What would I do with 48 cores

If I had access to 48 cores and 128 GB of RAM, I would use the computational power to resolve the more than half-century old Hirsch conjecture, which states that a polytope in 'd' dimensions with 'n' facets has a diameter less than 'n-d'. Example: for a cube in 3d, the cube has 6 facets. The diameter of the cube (the maximum distance between any 2 vertices) is 3. Thus atleast for the 3-cube Hirsch is true. Hirsch has also been shown to be true for d=4,5 and recently d=6. Using a cutting plane algorithm I have designed a combinatoric enumeration system which can generate all possible counter-examples to Hirsch, but since the number of polytopes is exponential and the enumeration requires significant computational power, no one has ever searched for counter-examples in high dimension, such as d=12. On d=7, the computer generation on a dual-Opteron 242 machine has been running for 8 months.
http://skoranne.blogspot.com/2010/03/more-polytope-experiments.html
http://skoranne.blogspot.com/2009/10/polytope-enumeration-system-hits-new.html
A 48 core machine with high speed memory connection would be sufficient in either (i) showing a counter example of Hirsch, or (ii) extending the known dimension where Hirsch is true upto 12.

In addition to being the single most fundamental problem in Operations Research, Hirsch, also has practical applications to Linear Programming. Any advances made in this domain would translate to immediate benefits in the simplex algorithm.

It is my opinion that rather than solve a single problem, such as climate modeling, or folding, or even natural resource and food resource scheduling for under-developed nations, we, as computer scientist should target the fundamental algorithms for optimization, which when improved, can benefit in providing better solutions to the complex problems we all face in the 21st century.

Python Polytope Perfect

I am a Common Lisp fan, so never bothered to look at Python in great detail until the need for polytope visulization and Anand's gentle prodding to try NetworkX and Ubigraph tempted me.

Python is so close to Lisp; it was almost like coming home. I picked up the syntax as I went along, and within 2 nights I had put together an interactive shell around the polytope explorer.

Example:

def CalculateHeritage( P, i ):

"""Given the polytope table and the polytope index find its heritage"""

answer = []

parentId = P[i].parentId

while i != parentId:

answer.append( (parentId, P[i].cut_set ) )

i = parentId

parentId = P[i].parentId

return answer

Anyone who has written lambda defuns, or docstrings can see the "inspiration", anyway who cares its good that they have implemented a good subset of Lisp.

Object-oriented programming is also there, ala, CLOS thrown on the existing language.

class Polytope:

"""Facets, Fvector, signature and parent information"""

def __init__(self):

self.facets = []

self.fvec = []

self.signature = ""

self.parent = 0

self.parendId = -1

self.cut_set = []

def dump(self):

print self.signature

print " "

print self.parent

print " "

print self.parentId

But the main advantage of using Python comes here:

def ParseFile( fileName ):

print "Reading file %s" %fileName

if polytope_file_name.find( '.gz' ) != -1:

file = gzip.open( fileName, 'rb' )

lines = file.readlines()

file.close()

else:

f = open( fileName, 'r' )

lines = f.readlines()

f.close()

Just using "import gzip" gave me the ability to compress my data set from 1 Gb to 65 Mb, and still retain the ability to use the data.

Using matplot and NetworkX I got the 4-pane visualizer; left top shows original

polytope, below it the induced cut-set, right top is the graph remainder and right

bottom is the produced polytope graph. You can iterate over the polytopes by specifying which vertices to truncate.

Anand thinks linear cuts will not increase the diameter and the interactive system has confirmed it so far, but the proof is worked on.

Summary: Python is like Lisp, I like Lisp => I like Python.

More polytope experiments

Anand has been visiting for the weekend and we have been working on enhancing the visualizer he has written to see the high dimensional polytopes. The enumeration software has also been enhanced and is much faster now.

Here is an example: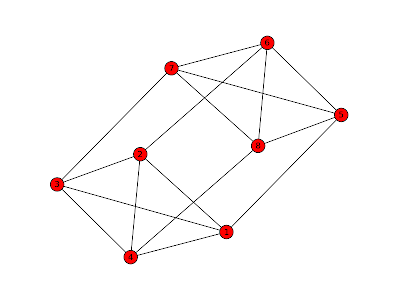This is the 4-prism generated from the 4-simplex by deleting any vertex. Now if we move a hyperplane to truncate vertices 3 and 7 we get

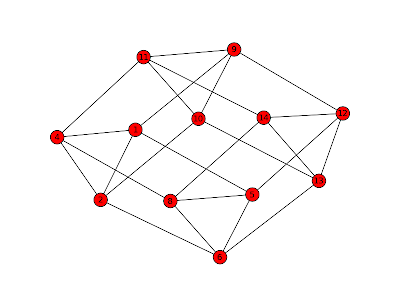The final cut is 4 vertices, { 4, 8, 11, 14 }. Truncating these gets us the beautiful 4-cube which I had alluded to in an earlier post.

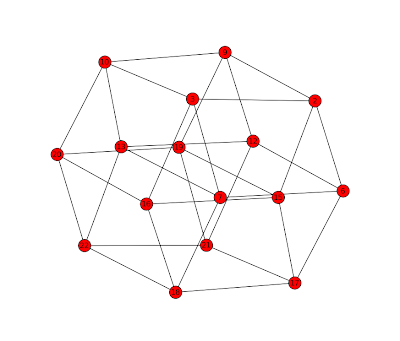
The actual face-lattice for the 4-cube produced by this cut is
VERTICES_IN_FACETS
{ 0 1 2 3 4 5 6 7}
{ 0 2 4 6 8 10 12 14}
{ 1 3 5 7 9 11 13 15}
{ 0 1 2 3 8 9 10 11}
{ 0 1 4 5 8 9 12 13}
{ 2 3 6 7 10 11 14 15}
{ 4 5 6 7 12 13 14 15}
{ 8 9 10 11 12 13 14 15}

If that is not poetry, I dont know what is. As Hardy had said "It must be true, as no one will have the imagination to invent something as beautiful....".

Cut sequence for the interactive enumerator are;
1
0
1
2
1 5
1
4
4 8 11 14
0

GCC 443 installed and running

Hello Readers*,

Just compiled and installed GCC 443 from SVN. Looks promising, especially the feature
with profile smoothening with parallel threads; will do some performance compares
and post.

* = Kleene closure for ZERO or MORE.

Polytope Enumeration System hits new high

Running for quite some time now we have got > 400K (d=5) polytopes and > 150K (d=7)
polytopes, alongwith their Face lattice.

Face lattice construction from VERTICES_IN_FACETS uses the co-atomic property of polytopes, that faces are proper intersection of facets;

Consider
VERTICES_IN_FACETS
{ 0 1 2 3 5 6 7 8 9 11 12 13 14 15}
{ 0 1 2 4 5 6 7 8 10 11 12 13 14 16}
{ 0 1 3 4 5 6 7 9 10 11 12 13 15 16}
{ 0 2 3 4 5 6 8 9 10 11 12 14 15 16}
{ 1 2 3 4 5 7 8 9 10 11 13 14 15 16}
{ 0 1 2 3 4 6 7 8 9 10}
{ 0 1 2 3 4 12 13 14 15 16}
{ 5 6 7 8 9 10}
{ 11 12 13 14 15 16}

Using "polymake" for reference gives us:
SIMPLE
1

DIAMETER
3

F_VECTOR
17 51 75 65 33 9

CD_INDEX
c^6 + 7c^4d + 24c^3dc + 39c^2dc^2 + 51c^2d^2 + 34cdc^3 + 85cdcd + 102cd^2c + 15dc^4 + 54dc^2d + 105dcdc + 75d^2c^2 + 102d^3

Also we get:
F2_VECTOR
17 102 255 340 255 102
102 51 255 510 510 255
255 255 75 300 450 300
340 510 300 65 195 195
255 510 450 195 33 66
102 255 300 195 66 9

SIMPLE
1

FLAG_VECTOR
1 17 51 75 255 65 340 510 33 255 510 450 1530

CD_INDEX_COEFFICIENTS
1 7 24 39 51 34 85 102 15 54 105 75 102

The constructed graph is:
GRAPH
{1 2 3 4 6 12}
{0 2 3 4 7 13}
{0 1 3 4 8 14}
{0 1 2 4 9 15}
{0 1 2 3 10 16}
{6 7 8 9 10 11}
{0 5 7 8 9 10}
{1 5 6 8 9 10}
{2 5 6 7 9 10}
{3 5 6 7 8 10}
{4 5 6 7 8 9}
{5 12 13 14 15 16}
{0 11 13 14 15 16}
{1 11 12 14 15 16}
{2 11 12 13 15 16}
{3 11 12 13 14 16}
{4 11 12 13 14 15}

Yohoo! another step towards full classification of simple polytopes using Cohen-Macaulay ring algebra.

$f$-vector inequalities for convex polytopes

During our (joint work with Anand Kulkarni) on polytope enumeration we have accumulated polytope datasets for d=3,4,5,6,7,8,9

The data sets from these experiments are being used to derive new $f$-vector inequalities.

Consider the following example:
1 F_VECTOR ( 10 25 30 20 7 1 )
1 F_VECTOR ( 12 30 34 21 7 1 )
1 F_VECTOR ( 14 35 40 25 8 1 )
2 F_VECTOR ( 16 40 44 26 8 1 )
3 F_VECTOR ( 18 45 48 27 8 1 )
3 F_VECTOR ( 18 45 50 30 9 1 )
2 F_VECTOR ( 20 50 52 28 8 1 )
7 F_VECTOR ( 20 50 54 31 9 1 )
15 F_VECTOR ( 22 55 58 32 9 1 )
7 F_VECTOR ( 22 55 60 35 10 1 )
28 F_VECTOR ( 24 60 62 33 9 1 )
34 F_VECTOR ( 24 60 64 36 10 1 )
25 F_VECTOR ( 26 65 66 34 9 1 )
116 F_VECTOR ( 26 65 68 37 10 1 )
1 F_VECTOR ( 28 70 68 34 9 1 )
1 F_VECTOR ( 28 70 69 34 9 1 )
36 F_VECTOR ( 28 70 70 35 9 1 )
350 F_VECTOR ( 28 70 72 38 10 1 )
1 F_VECTOR ( 28 70 73 39 10 1 )
1 F_VECTOR ( 30 75 72 35 9 1 )
2 F_VECTOR ( 30 75 73 35 9 1 )
19 F_VECTOR ( 30 75 74 36 9 1 )
596 F_VECTOR ( 30 75 76 39 10 1 )
3 F_VECTOR ( 30 75 77 40 10 1 )
9 F_VECTOR ( 32 80 78 39 10 1 )
11 F_VECTOR ( 32 80 79 39 10 1 )
1252 F_VECTOR ( 32 80 80 40 10 1 )
7 F_VECTOR ( 32 80 81 41 10 1 )
18 F_VECTOR ( 34 85 82 40 10 1 )
39 F_VECTOR ( 34 85 83 40 10 1 )
2 F_VECTOR ( 34 85 83 41 10 1 )
1575 F_VECTOR ( 34 85 84 41 10 1 )
22 F_VECTOR ( 34 85 85 42 10 1 )
16 F_VECTOR ( 36 90 86 41 10 1 )
37 F_VECTOR ( 36 90 87 41 10 1 )
7 F_VECTOR ( 36 90 87 42 10 1 )
1212 F_VECTOR ( 36 90 88 42 10 1 )
42 F_VECTOR ( 36 90 89 43 10 1 )
60 F_VECTOR ( 38 95 90 42 10 1 )
75 F_VECTOR ( 38 95 91 42 10 1 )
16 F_VECTOR ( 38 95 91 43 10 1 )
1170 F_VECTOR ( 38 95 92 43 10 1 )
43 F_VECTOR ( 38 95 93 44 10 1 )
1 F_VECTOR ( 40 100 93 42 10 1 )
61 F_VECTOR ( 40 100 94 43 10 1 )
162 F_VECTOR ( 40 100 95 43 10 1 )
10 F_VECTOR ( 40 100 95 44 10 1 )
756 F_VECTOR ( 40 100 96 44 10 1 )
1 F_VECTOR ( 42 105 100 44 10 1 )
203 F_VECTOR ( 42 105 100 45 10 1 )
4 F_VECTOR ( 42 105 97 43 10 1 )
45 F_VECTOR ( 42 105 98 44 10 1 )
183 F_VECTOR ( 42 105 99 44 10 1 )
2 F_VECTOR ( 44 110 100 44 10 1 )
6 F_VECTOR ( 44 110 101 44 10 1 )
34 F_VECTOR ( 44 110 103 45 10 1 )
1 F_VECTOR ( 6 15 20 15 6 1 )


Analyzing this set of 5d polytopes we can get many linear inequalities, the hope is to get new ones which are hitherto unknown, something like

6f_3 + 2f_2 < 8(f_0+f_4)

Compiler Optimizations and Machines

Sun Studio 12u1 running Solaris 10 SPARC

My Ultra 5 has been running Solaris 10 and has been my primary SSH and Web server. I used it to do compiler optimizations for RISC machines and now that a new idea for code optimization has been formulated (see other posts) I am getting ready to try it first on the SPARC IIi.

The list of machines I am using for code optimizations are:

1) Opteron 242 running Gentoo Linux,
2) SPARC IIi Ultra 5 Solaris 10
3) Intel Pentium M Centrino running Fedora Core 10 (Laptop)
4) PowerPC 970 (2 EMT) in PlayStation 3 running YellowDog Linux 6.2
5) Opteron running Solaris 10 (x86_64) real and virtual
6) MIPS (Emotion Engine PS2) running Linux: deprecated
7) Embedded ARM : deprecated